【ベストコレクション】 算数 魔 方陣 問題 120396-算数 魔方陣 問題

Mixi中学受験の質問箱＆よろず相談所 算数「魔方陣・円陣・星陣」の解き方 「魔方陣・円陣・星陣」の問題が、公立中高一貫校適性検査問題集に載っていました。 数字の組合せ等を考えてると、かなり時間がかかってしまいます。 小学6年生にも説明出来て、時間をかけずに簡単に解ける 立体魔方陣（06年ジュニア算数オリンピック、トライアル問題より） 硬貨の魔方陣、解けますか？ （第7回算数オリンピック、トライアル問題より）中学受験算数問題（桜蔭 04）中学受験算数問題（Weekly SapiX）げた箱の入れ方（四谷大塚 第1回合不合判定テストより）電車と時刻表（雙葉中学 受験算数問題 09年）選挙の論理計算（四谷大塚 第3回合不合判定テストより）結び目はどこ？

実践記録算数５ ６年

算数 魔方陣 問題

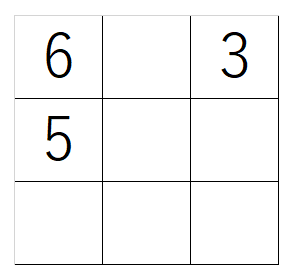
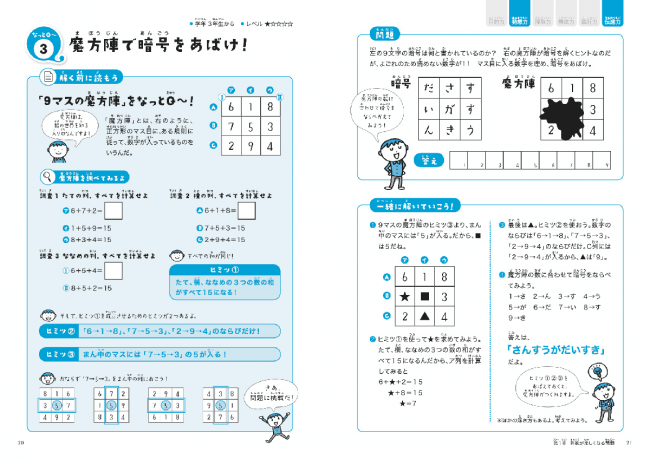
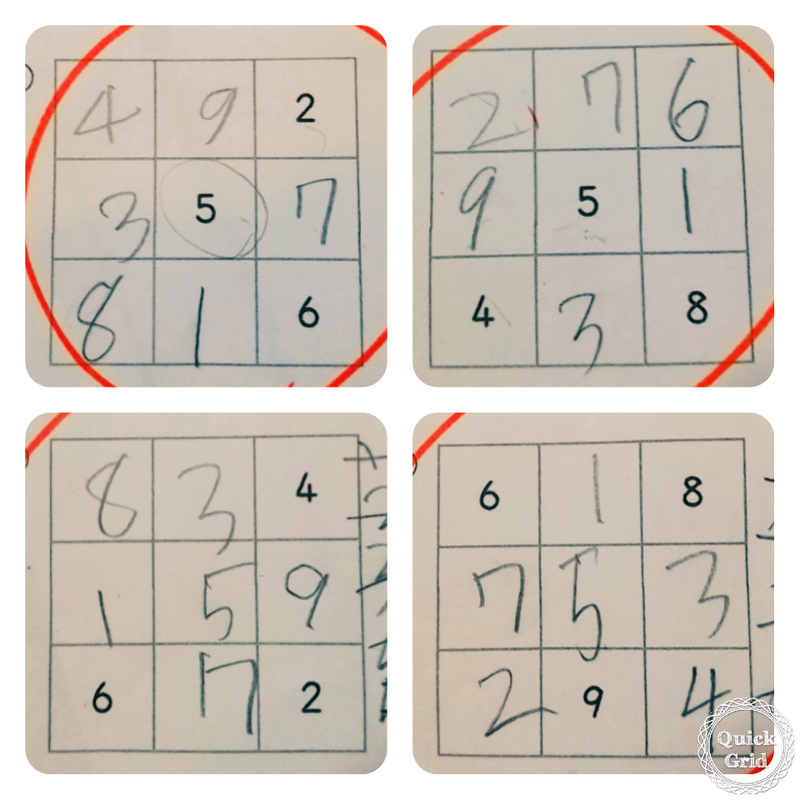
算数 魔方陣 問題- 無料プリントダウンロード画面 たて、よこ、ななめの、どの3つの数字を足しても15になるように、1～9の数字を空いている に入れていくという作業です。 問題レベルは、①が易しい問題で④になるにしたがって難しくなってます。 魔方陣のルール 魔方陣には以下のようなルールがあります。 表に1からマス目の総数までの数字を配置し、同じ数字を2度と使わないこと 計算結果は紙に書き出されること 最も基本的な縦横3列の魔方陣は、3次の方陣または3方陣とよばれ、縦、横、斜めの

算数クイズ 冷静にサクッと解きたい魔方陣の良問 子供から大人まで動画で脳トレ 楽天ブログ

* 魔方陣でスライドパズル * クロスワードっぽい魔方陣の問題 * 魔方陣 ID ・魔方陣ってなに 魔方陣とはn行n列のマスに 1～n 2 の数をいれて、すべての行、列、そして2つの対角線上の数の和が等しくなるものです。nは3以上の場合を考えます。算数オリンピック委員会監修 今回の問題は、「最小数の魔方陣」という条件がついているため、一筋縄では いかないところが、さすが、広中杯ですね。 解答・その7 （ペンネ－ム：T_Tatekawa） Ⅰ 魔方陣とは 「まほうじん」と聞くと、ゲーム等で出てくる「魔法陣」を思い浮かべる方もいますが、数学の「まほうじん」は 魔法の四角形 という意味合いで「魔方陣」と書きます。 英語にすると"magic square " です。 まずは、この魔方陣の定義を確認しておきましょう。

 平均＝仮平均＋差の平均 魔方陣 「たて」「横」「斜め」で 求められるところを見つける かずのかず 以上、「数学嫌いな人が、 数学を楽しく好きになって欲しい」 かずのかずでした 中1数学「正負の数の乗法 除法」の問題 どこよりも簡単な解き35 27 22 4 3; 今回は3×3魔方陣に隠された面白い性質について紹介します。 Ⅰ 両端平方和の法則 Ⅱ 中央積和の法則 ★魔方陣の関連記事はこちら↓★ ・「3×3の魔方陣の作り方」 ・「3×3魔方陣のすごい性質」 ・「積の魔方陣」 ・「3×3×3の立方陣」（立体バージョンの魔方陣） Ⅰ 両端平方和の法則 以前

19 5 13 33 18 23;算数の問題、身につけてほしい習慣 こんにちは。 さて、そのまま真面目に、今日は算数の問題のはなし。 すでにチャレンジタッチ2年先取りで、4年生の5月のメインレッスン終わった長男。 昨日、挑戦レッスンに、2年生のドリルで出てきた魔方陣が出て9 28 21 16 8 29;

数楽 大人でも解けない算数 魔方陣 Vol 3 Kec近畿予備校 Kec近畿教育学院 公式ブログ

小学生でも解ける 算数クイズ その11 魔方陣 脳トレ 脳幹を64倍活性化

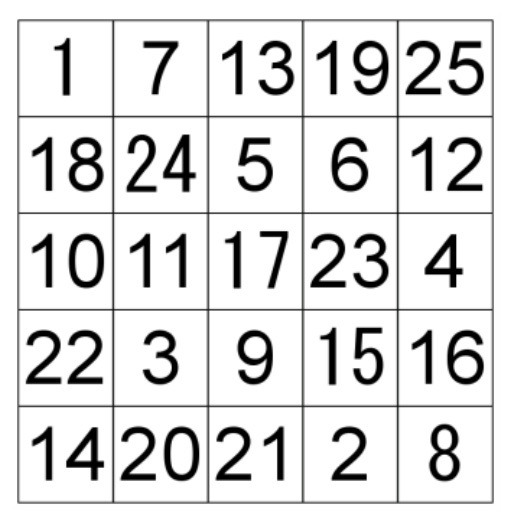
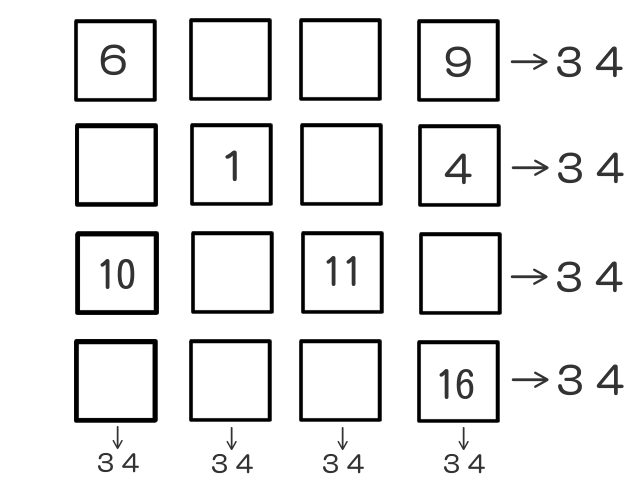
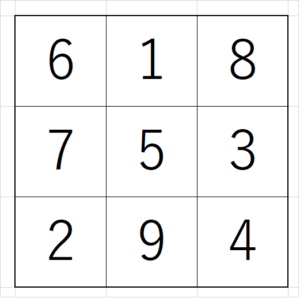
4マス×4マスの魔方陣とは 1から16の数字で出来ています。 「縦」に並ぶ4個の数字の合計、「横」に並ぶ4個の数字の合計、「斜め」に並ぶ4個の数字の合計が全て34になる不思議な図形です。 詳しい魔法陣の法則はこちら 広告 問題012 （21年5月18日 追加 だれでも作れる4 4の魔方陣 公務員試験に役立つ算数 数学3×3の魔方陣 右の魔方陣は，縦3個×横3個の9個の正方形のマスを作って， 1～9の数を入れたものです。 ①どこをたしても15 3×3の魔方陣では，縦，横，斜めの数の和がすべて15になります。 その理由は，1～9の数を順にたすと，その和は45。

算数パズル 意外と解けない魔方陣の基本問題 理論的に解きましょう Youtube

実践記録算数５ ６年

魔方陣を提示した後，右の問題を提示する。 T 「さあ，これが何か知ってますか。」 C 「魔方陣！」 C 「先生，魔方陣って聞いたことあるよ。」 C 「たすと同じ数になるのでしょ。」 C 「縦，横，ななめ，どこをたしても同じ数になるんだよね。」 C 5×5マスの魔方陣で 24 8 5 14 16 4 11 25 9 の中の数を求めるものです いろいろ考えましたがわかりませんでした。 解き方含めおしえてください おねがいします ベストアンサー 数学・算数 九宮魔方陣 7．8年前琉球大学にいらした「ミヤギサトシ」という 前提･･･魔方陣は1〜9だけではありませんよ！そして、出題ミスではなく普通にいい問題です。 因みに、1〜9の魔方陣は、 真ん中→5 四つ角→2、4、6、8 辺の所→1、3、5、7 と決まっている(これ以外は作れない)ので、この問題は違うことが分かります。

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

算数 167 魔方陣の一部を上手く計算しよう 附設 数の性質 Youtube

魔方陣 第15問 （筑波大学附属中学 入試問題 14年（平成26年度） 算数） 問題 （筑波大学附属中学 入試問題 14年 算数） 難易度★★ 下の図のマスの中には、0から8までの整数が1つずつ 入ります。 縦と横それぞれの合計が全て等しくなるように 全てのみんなの算数オンライン 中学受験 4年 推理 中学受験 4年 unit 303 推理 魔方陣 確認テスト ログインが必要です フィードバック(不具合・誤記・問題解法の矛盾に関する連絡) 算数問題 一覧算数 魔方陣たて、よこ、ななめの、どの3つの数字を足しても15になるように、1～9の数字を埋めていくと言う問題です。介護予防の脳トレにどうぞ。高齢者 算数魔方陣①④百マス計算単純に100マスあるので100問はできる百マスの計

３ ３の魔方陣 わくわく さんすう子育て 幼児さんすうインストラクター曽山桂子のブログ

びっくり Com

 平均の魔方陣（11年算数オリンピック、ファイナル問題から） 5つの輪の和がすべて等しくするには？ （第2回算数オリンピック、予選問題から） たてと横の数字の和をみな等しく！ （11年ジュニア算数オリンピック、ファイナル問題より） 真ん中に魔方陣の例 魔法陣小学生, 小学生算数魔方陣の解き方に教え方 クリックして Bing でレビューする2106 この動画では小学3年生の次女のたぬりに中学1年生のコッコが算数の魔方陣の解き方を教えている様子をご視聴頂けます。 著者 コッコママ23 6 19 2 15;10 12 19 21 3;魔方陣 第15問 （筑波大学附属中学 入試問題 14年（平成26年度） 算数） 問題 （筑波大学附属中学 入試問題 14年 算数） 難易度★★ 下の図のマスの中には、0から8までの整数が1つずつ 入ります。

びっくり Com

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

 推理の問題の基本はツールの利用です。 つまり、問題を見てどんなツールを利用するのか特定できないと話になりません。 問題のパターンは4つ覚えておくといいでしょう。 1大きい、小さいを推理する（順番） 2魔方陣 3勝敗表 4順位表魔方陣の難問！ （東大寺学園中学 06年） ;Hello School 算数 方陣算 練習問題 解答と解説 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

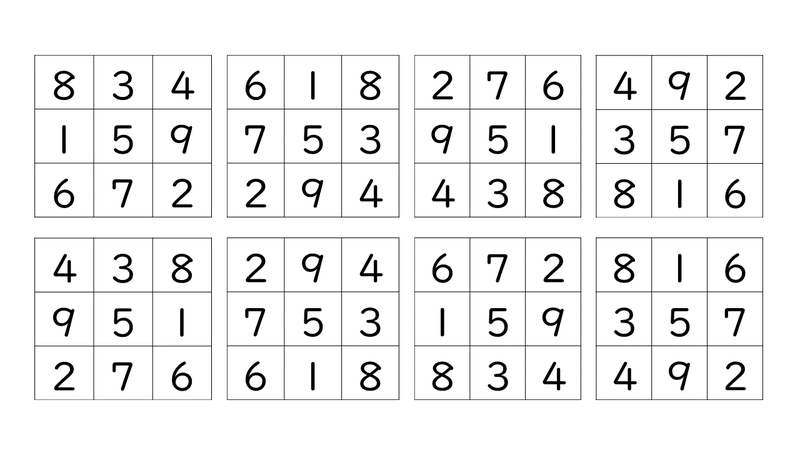
だれでも作れる4 4の魔方陣 公務員試験に役立つ算数 数学

 方陣算の記事一覧 方陣算まとめ(この記事) 中実方陣 中空方陣 三角形に並べる 多角形に並べる「方陣算」を学習している中学受験生の方「石がたくさん並んでいて面倒くさく、難しそう」と思っていませんか？実は、ちょっとした図を書くだけで方陣算は 魔方陣の学習①＃算数＃スーパーエリート 魔方陣は中学受験の算数では、頻出の問題です。 でネット検索をすると、膨大な量の過去問題を見つけることができます。 過去問題を見てみると、約数や比、素数を使った魔方陣、空白の多い魔方陣から一列の17 7 11 30 15 31;

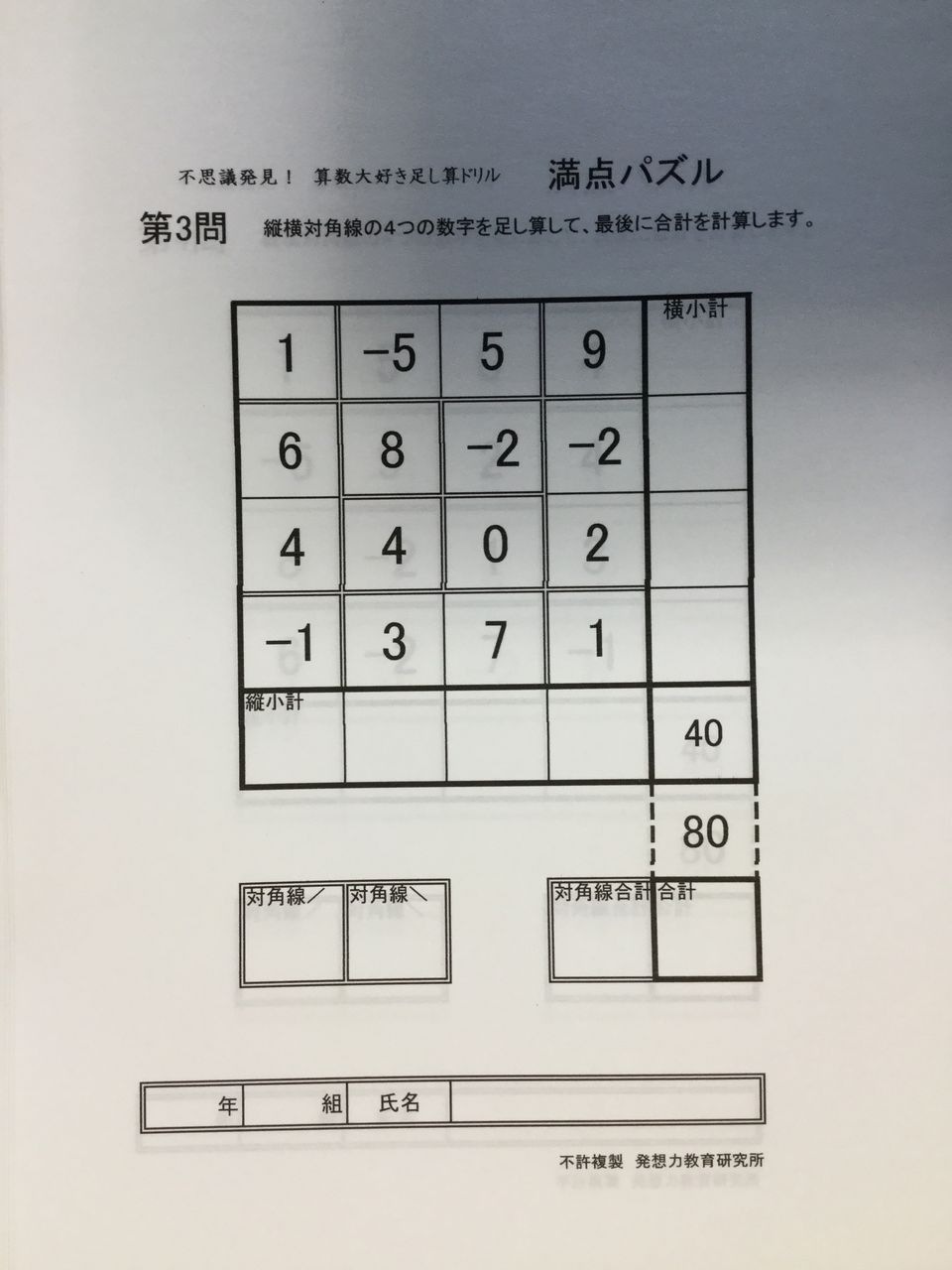
夏休み自由研究２０１９ 小学二年生から魔方陣の不思議な力で算数大好き足し算脳トレ 満点パズル足し算ドリル１００問完成 発想力教育研究所 素数誕生のメカニズム

まほうじんを作ろう 家庭学習レシピ

受験研究社 × ちびむすドリル コラボ企画天才脳ドリル 学びのセンスを鍛えよう！～まったく新しい脳力開発ドリル～幼児用教材から小学・中学・高校生用の学習参考書・問題集を出版している増進堂･受験研究社。子どもがこれからの人生を生き抜くために必要なもの、それは「物事を最後の問題はたて・横・ななめの数をたすのではなく、かける魔方陣です。考え方のポイントは同じです。 数の組み合わせで考えて、数が限定されるところから、 うめていきましょう。 まず、中央の十字に注目してみます。3×3＝9マスの魔方陣 02 9 1 11 魔方陣 2 「パズルより面白い中学入試の算数」 （1994年） = 講談社 「ピーター・フランクルの算数名問題」 （1995年） = 講談社

魔方陣 中学受験ー算数解き方ポータル

魔方陣 算数オリンピック問題に挑戦

たて3マス・横3マスの，合計9マスの魔方陣だ からといって，必ずしも1～9の数が入っていると は限りません。 右の図のように，大きい数が入っ ている場合もあります。 では，ちょっとむずかしい魔方陣の問題について， 学習していきましょう。 いくつかの過去問を見ると，どうも 問題の魔方陣はとても安易な方法で作られている ようです。 次に，簡単な4×4の魔方陣の作り方を紹介します。 この出題の魔方陣は， ヨコ2列を入れかえたものを，左右逆にしただけ ですから，Aが5で，Bが13です。 な 魔方陣 第14問 （灘中学 入試問題 14年（平成26年度） 算数） 問題 （灘中学 入試問題 14年 算数） 難易度★★★★ 縦横に並んだ の中に数を入れていきます。 ただし、1つの がその上下左右にある 4つの と短い線でつながって いるとき、これら 5つの の

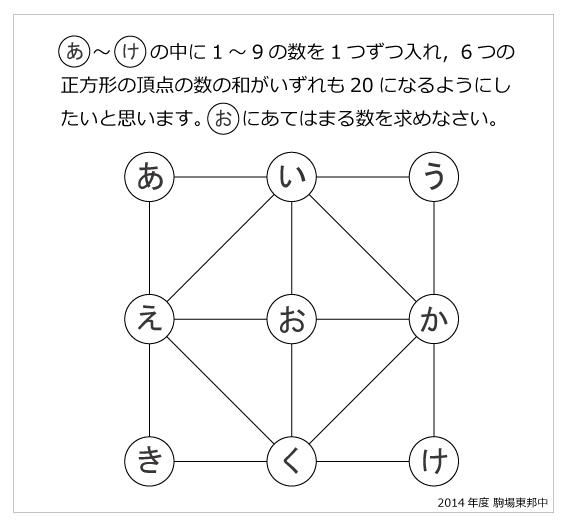
今年 ２０１４年の駒場東邦中学の入試問題から 魔方陣の推理パズル パズル算数クイズ

積が等しくなる魔方陣 ２００５年算数オリンピック トライアル問題より 算数オリンピック問題に挑戦

 (06年算数オリンピック、トライアル問題)」 あることに気づけば少しの計算でサクッと解ける面白い問題です。 ポイントはまわりのマスに入る数の和です。 脳トレとして最適ですよ。 おまけ問題も魔方陣で良問なのでこちらもぜひ挑戦してみてください。

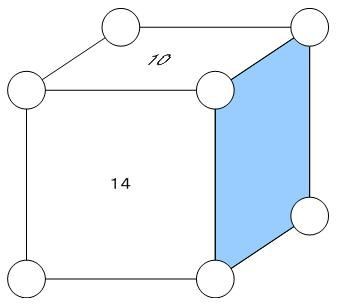
立体魔方陣 豊島岡女子学園中学 06年 イメージでわかる中学受験算数問題

魔方陣のとても簡単な作り方 コツが分かれば小学生でも作れます

東大生が考えた魔法の算数ノート なっとq を無償公開 株式会社レヴィのプレスリリース

楽しい算数の授業 10年5月号 算数が好きになる問題 ６年 分数魔方陣

算数クイズ 冷静にサクッと解きたい魔方陣の良問 子供から大人まで動画で脳トレ 楽天ブログ

魔方陣 算数星人のweb問題集 中学受験算数の問題に挑戦

魔方陣の学習 算数 スーパーエリート 23年中学受験 無分別が虎口前の肝要なり

魔方陣 パズル算数クイズ

魔方陣 Wikipedia

1

魔方陣問題 パズル おもしろ算数問題

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

魔方陣を作ってみよう おもしろ科学実験室 工学のふしぎな世界 国立大学56工学系学部hp

魔方陣 8月説明会の詳細 キュービックブログ

高齢者 算数魔方陣

はじめての魔方陣 和洋 柴田 本 通販 Amazon

魔方陣 解けるかな 算数の難問に挑戦

中学受験算数 あなたは解ける 特殊な魔方陣の超簡単な解き方 学習院中学08入試問題 毎日１題中学受験算数５９ Youtube

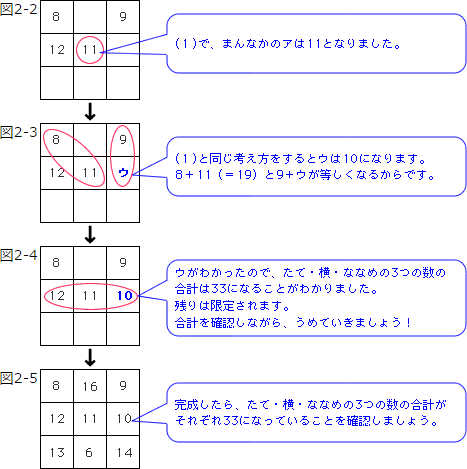
魔方陣 まほうじん 算数の教え上手 学びの場 Com

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

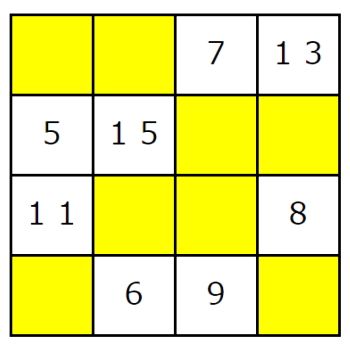
数字穴埋めパズル ４ ４魔方陣

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

中学受験算数 これだけ 算数のカギ 数と計算 魔方陣 ３ ３ Spi Youtube

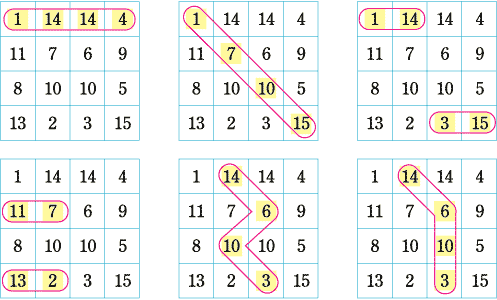
実践記録算数５ ６年

3

中学受験算数 ４ ４魔方陣を瞬殺できるチート技 誰でも解けます 毎日１題中学受験算数５４ Youtube

びっくり Com

３ ３の魔方陣 わくわく さんすう子育て 幼児さんすうインストラクター曽山桂子のブログ

魔方陣 マス目を使った数学パズル 空間情報クラブ 株式会社インフォマティクス

1

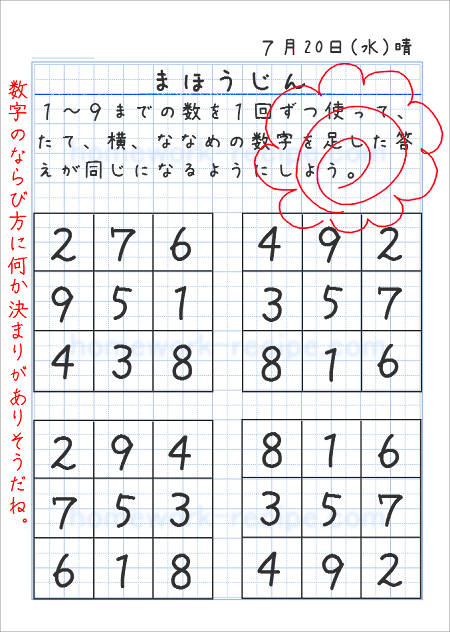
まほうじんを作ろう 家庭学習レシピ

3 3魔方陣問題の考え方と解き方と作り方 色々な感想とネタバレとit

魔方陣 頭の回転が問われる算数問題 Youtube

高1がスパコンで5 5魔方陣の全解に成功 2時間36分で2億7 530万5 224通り リセマム

算数パズル 意外と解けない魔方陣の基本問題 理論的に解きましょう Youtube

魔方陣のこと 西宮の塾なら個別指導かなえ塾

高1がスパコンで5 5魔方陣の全解に成功 2時間36分で2億7 530万5 224通り 4枚目の写真 画像 リセマム

4 4の魔方陣の解き方を教えて下さい画像は載せられませんので 左上 16右上 Yahoo 知恵袋

魔方陣 中学受験ー算数解き方ポータル

３ ３の魔方陣 わくわく さんすう子育て 幼児さんすうインストラクター曽山桂子のブログ

小学5年生の娘の宿題でこちらの魔方陣の問題が出たのですが 恥ずかしな Yahoo 知恵袋

魔法陣他 穴埋め問題４問 他２つ ０ 10 25 115 0965 Jyankquiz

魔法陣 ひろしんぼnow

高齢者 算数魔方陣

ひらめき算数１分パズル 魔方陣 筑波大学附属中学 ２０１４年 大人だって解ける 受験算数

魔方陣 第３問 立教新座中学 07年 平成19年度 入試算数問題 まいにち一題 中学受験過去問題研究

だれでも作れる4 4の魔方陣 公務員試験に役立つ算数 数学

中学受験 算数の学び方 受験生かそうでないかで どう違う 前編 アベブログ

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

アに入る数字は ２００６年算数オリンピック トライアル問題より 算数オリンピック問題に挑戦

3

楽しい算数の授業 10年5月号 算数が好きになる問題 ６年 分数魔方陣

ピグマリオン家庭学習 第４講座 魔法陣 ４ ４ 理系ママの家庭学習 家庭保育園からピグマリオンへ カホっ子の小学校受験と中学受験

魔方陣 レシピ 作り方 パズル

魔方陣 頭の回転が問われる算数問題 Youtube

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

ドリルズ 小学6年生 算数 の無料学習プリント魔法陣の問題

平均の魔方陣 ２０１１年算数オリンピック ファイナル問題から 中学受験ー算数解き方ポータル

魔方陣 算数星人のweb問題集 中学受験算数の問題に挑戦

魔方陣 マス目を使った数学パズル 空間情報クラブ 株式会社インフォマティクス

魔方陣のとても簡単な作り方 コツが分かれば小学生でも作れます

魔方陣の問題を教えてください 小学2年生 4年生が対象のパズル道場という Yahoo 知恵袋

算数 魔 方陣 問題

魔方陣を作ってみよう おもしろ科学実験室 工学のふしぎな世界 国立大学56工学系学部hp

魔方陣をとくコツってありますか 小学３年生 小3 の問題集に出てきました 息 Yahoo 知恵袋

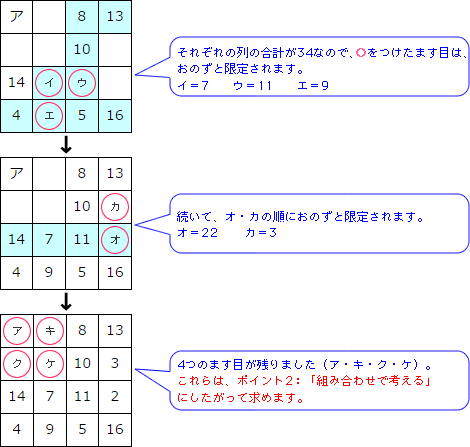
魔方陣 まほうじん 算数の教え上手 学びの場 Com

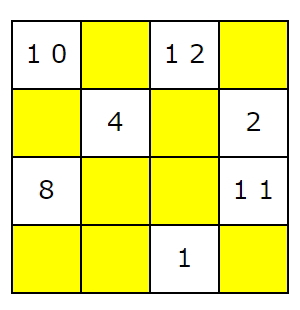
数字穴埋めパズル ４ ４魔方陣

算数レベルの魔方陣 30秒以内に解きたい魔方陣 Youtube

まほうじんを作ろう 家庭学習レシピ

中学受験算数 魔方陣を超きもち良く論理的に解く 駒場東邦中学14入試問題 毎日１題中学受験算数６０ Youtube

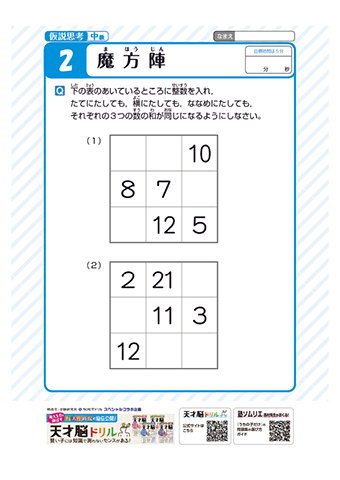
中級 仮説思考 未等式 魔法陣 推理算 四角に分ける ビルディング ナンバープレイス 対象学年 小学全学年 天才脳ドリル 無料ダウンロード ちびむすドリル 小学生

びっくり Com

高校入試の魔方陣 最低限の計算で解いてみてください 暇つぶしに動画で脳トレ

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

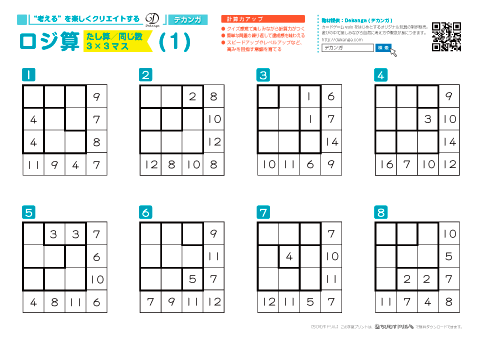
小学生の算数クイズ パズル 問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生

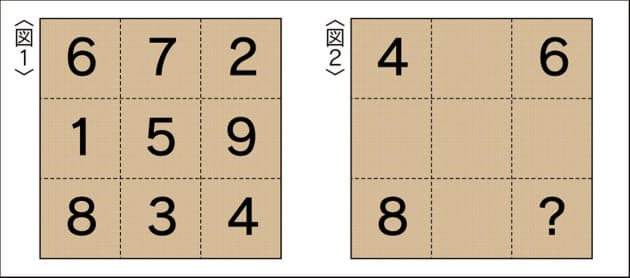
算数オリンピックに挑戦 第19回 Nikkei Style

中学受験算数 魔方陣は感覚 いいえ理論です 毎日１題 中学受験算数９ Youtube

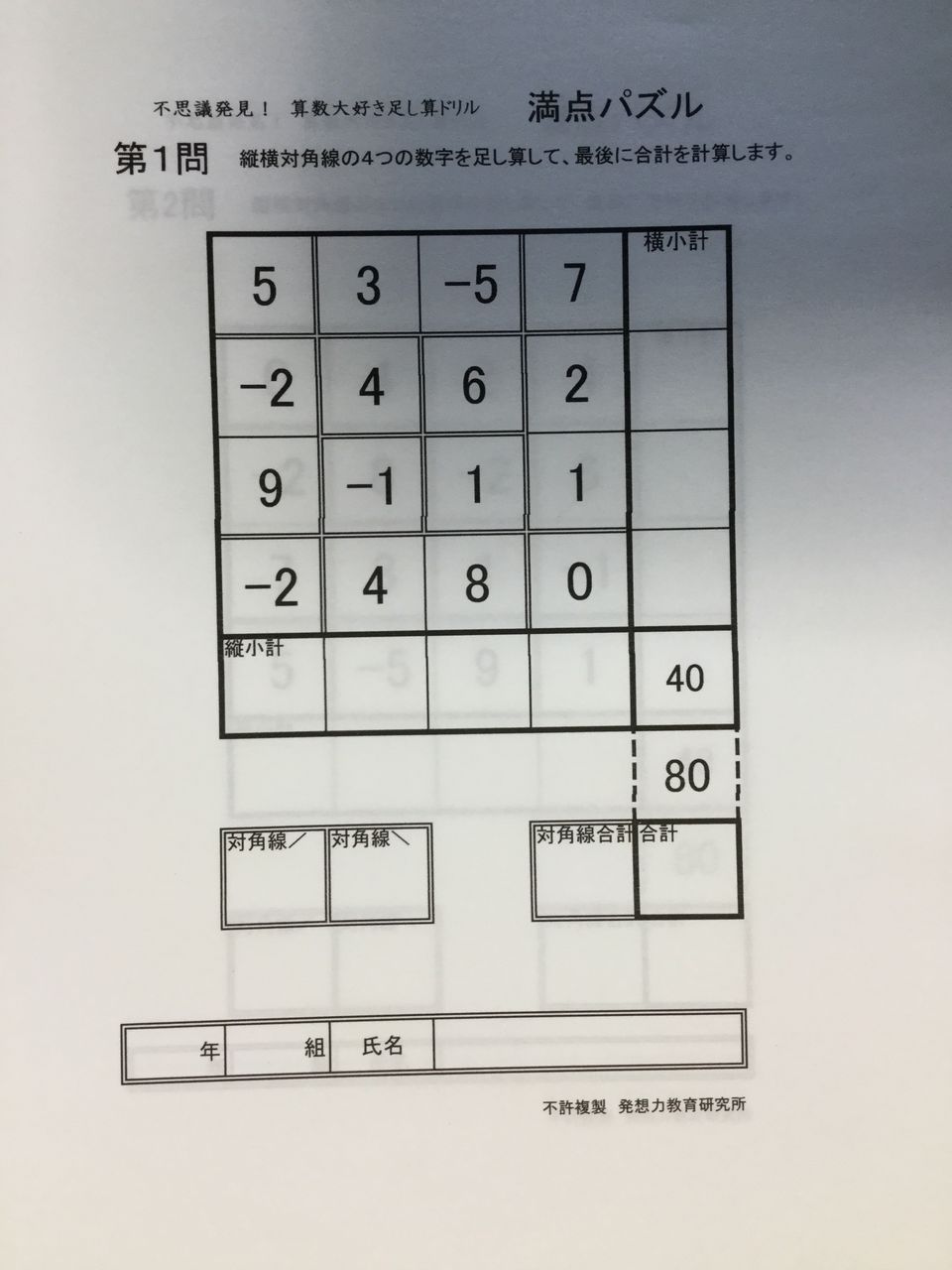
夏休み自由研究２０１９ 小学二年生から魔方陣の不思議な力で算数大好き足し算脳トレ 満点パズル足し算ドリル１００問完成 発想力教育研究所 素数誕生のメカニズム

小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト

小学2年生の家庭学習 ピグマリオンの魔方陣で悶絶しています ママ お勉強がしたいの

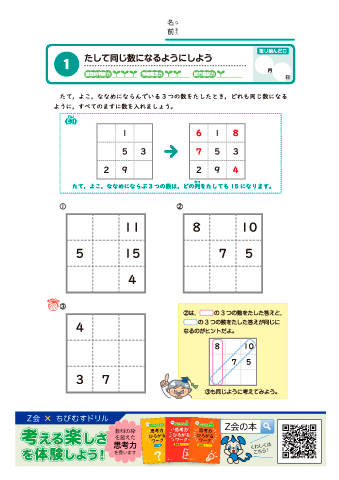
小学生の算数クイズ パズル 問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生

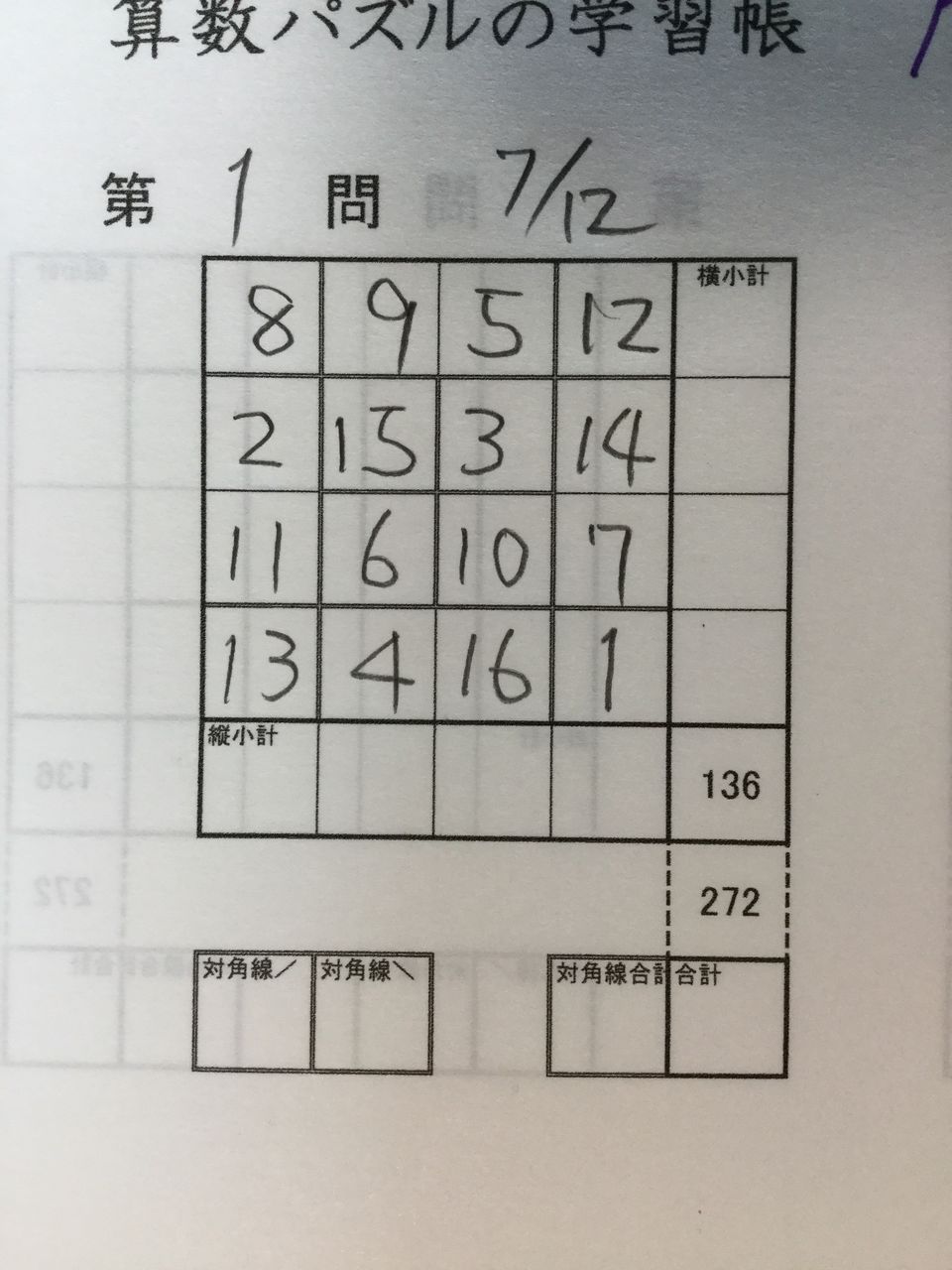
夏休み自由研究２０１９ 魔方陣を作ろう １６マス計算魔方陣足し算ドリル開発中 発想力教育研究所

同じにならない魔方陣 12年算数オリンピック ファイナル問題より 算数オリンピック問題に挑戦

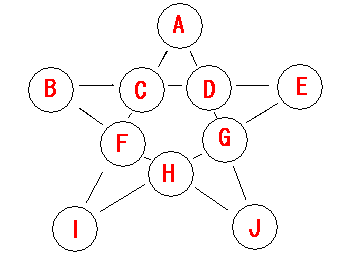
今週の問題 第１０回 変形魔方陣 その２ 解答 走り続けるｍａｚｒａ日記 楽天ブログ

魔方陣のとても簡単な作り方 コツが分かれば小学生でも作れます

Incoming Term: 算数 魔方陣 問題,